

"Limiting the use of creativity in the classroom reduces mathematics to a set of skills to master and rules to memorize. Doing so causes many children's natural curiosity and enthusiasm for mathematics to disappear as they get older, creating a tremendous problem for mathematics educators who are trying to instill these very qualities." - Hartwig Meissner, Creativity in Mathematics Education
Most adults remember math instruction as listening to a teacher’s explanation followed by lots of rote practice. This focus on memorizing procedures without context and deep understanding resulted in an adult population that largely feels they are “bad at math.” This negative memory has resulted in a profound cultural dislike of math, contributing to our current situation of too few students choosing to become much-needed mathematicians and engineers.
Changes elicited by the Common Core State Standards and the growing popularity of the Singapore Math approach have generated significant change to math instruction in the elementary classroom. Rather than an approach that focused on finding the answer to 4+4, students are now asked to share many ways they can make the value 8.
While 4+4 will likely be the first option shared, it won't take long for students to come up with other factors like 2+6, 1+7, and 3+5. Students may not be able to define the commutative property of addition, but they will realize that 6+2, 7+1, and 5+3 are also valid responses.
More time is required for students to begin producing responses like 12-4, but instead of telling students what to think, teachers now give them the opportunity to reason. As soon as an alternative to simple addition is suggested, the wave of new solutions grows almost exponentially.
A renewed focus on students explaining their work helps teachers determine whether learners understand concepts. Time that used to be spent on rote repetition of a procedure is now spent on arranging, rearranging, and thinking about a problem. The implicit message of “what's another way” is accepted so long as students can demonstrate the mathematical thinking behind their suggestions.
The use of base-ten blocks and Cuisinaire rods, created in the 1920’s, are not new. Their use in modern classrooms provides students a way to conceptualize numbers in a variety of ways. These tangible objects are called manipulatives.
If you are unfamiliar with the term, think about counting money. With money, each physical coin represents a value. Manipulatives like these provide a way for students to see and feel a mathematical concept by manipulating it. This hands-on, visual approach has been show to have a positive effect on student achievement. (Ruzic & O'Connell , 2001)
The prevalence of technology in the classroom introduces the concept of virtual manipulatives. Although they are not tangible, digital manipulatives can still be grouped and regrouped to create models that help students see and internalize mathematical concepts. Following is a sampling of the virtual manipulatives found in Wixie.
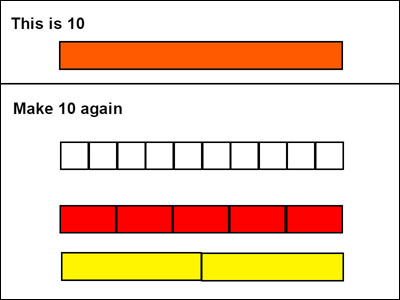
In the same way that student can move Cuisenaire rods on a table to form equal values; students can arrange representations to achieve the same effect using a computer. As they see and play with different ways to formulate the same value, they build stronger number sense and a better conceptual understanding of factors. As students play with virtual manipulatives, they build cognitive models that teachers can actually see, allowing them to quickly perform formative assessments and identify misconceptions.
Virtual manipulatives offer easy opportunities for constructing with shapes. As students participate in this type of play , they naturally sort, compare, match, and begin to create patterns, exactly the sort of mathematical thinking outlined in the Common Core State Standard for Mathematical Practice: 7. Look for and make use of structure.

Dr. Walter Drew and Dr. Henry Olds found benefits to building mathematical thinking as students first build patterns with physical shapes and then continue their work with the resulting patterns on the computer where they experimented further "in an environment where the risk factor is substantially reduced. Trying out ideas is faster and easier and mistakes or wrong turns are easily undone" when students work with virtual manipulatives. The resulting iconic pattern play helps students begin to understand how to apply elements of geometric patterns like rotation and reflection in a way that is both engaging and beautiful.
Using art is a great way to help students see the beauty of math as well as help them connect math to the world around them. Most students have seen tessellations in tiled bathrooms, kitchens, or courtyards. Many are also familiar with the work of M.C. Escher. Students can use the paint tools in programs like Wixie to create tiling patterns as well as their own original tessellations.

Wixie’s paint tools also let students play with symmetry in photos and even paint using linear and radial symmetry.

As they play with math on the computer through art and virtual manipulatives, students begin to create and solve their own problems. Creative digital tools provide a safe place they can experiment and easily undo mistakes. This environment encourages learners to try new approaches and “fail forward” as they work to solve problems they create.
Creative technology tools can help us foster and support a classroom culture that values multiple approaches, questions more than answers, process more than product. Encouraging creativity in math instruction can help us develop mathematical thinkers who have the “resourcefulness, persistence, and desire to explore alternative methods of solution.” (Mann, 2005) In other words, we can create a generation of students who love to play with math.
Mann, E. L. (2005). Mathematical Creativity and School Mathematics: Indicators of Mathematical Creativity in Middle School Students. University of Connecticut.
Meissner, H. (2000, July-August). Creativity in mathematics education. Paper presented at the meeting of the International Congress on Mathematical Education, Tokyo.
Ruzic, R. & O'Conell, K. (2001). "Manipulatives." Enhancement literature review.
Piggott, J. (2011). "Cultivating Creativity." University of Cambridge.
Creative classroom ideas delivered straight to your in box once a month.
New approaches to math improve fluency through the use of creative technology tools.

Get this FREE guide that includes:


Wixie
Share your ideas, imagination, and understanding through writing, art, voice, and video.
Rubric Maker
Create custom rubrics for your classroom.

Pics4Learning
A curated, copyright-friendly image library that is safe and free for education.
Wriddle
Write, record, and illustrate a sentence.

EDU ToDo
Interactive digital worksheets for grades K-8 to use in Brightspace or Canvas.
Topics